Leetcode 863. All Nodes Distance K in Binary Tree (Python)

Related Topic

Depth-First-Search. Breadth-First-Search.

Description

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.

Sample I/O

Example 1

Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2

Output: [7,4,1]

Explanation: 
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.

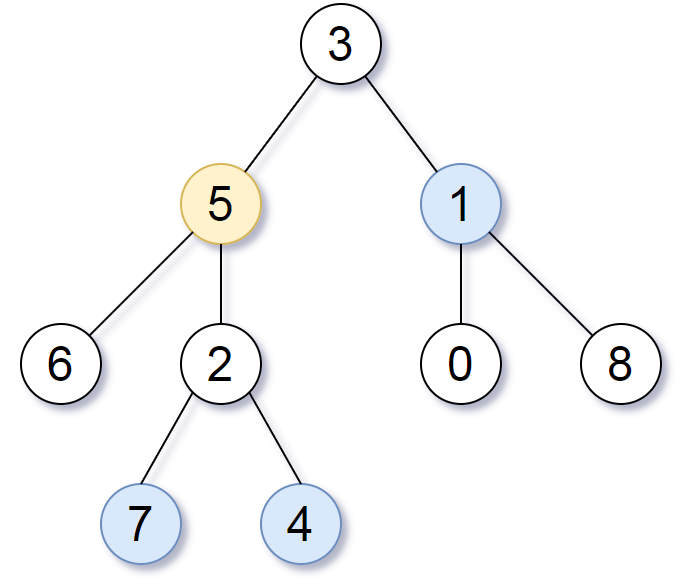
Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

Note

• The given tree is non-empty.
• Each node in the tree has unique values 0 <= node.val <= 500.
• The target node is a node in the tree.
• 0 <= K <= 1000.

Methodology

First use DFS to construct a graph like dictionary and then use BFS to iterate K levels start from the target point.

Code(DFS)

def distanceK(self, root, target, K):
        """
        :type root: TreeNode
        :type target: TreeNode
        :type K: int
        :rtype: List[int]
        """
        graph = collections.defaultdict(list)
        def dfs(parent,child):
            if child is None: return
            if parent and child:
                graph[child.val].append(parent.val)
                graph[parent.val].append(child.val)
            dfs(child, child.left)
            dfs(child, child.right)
            return
        
        dfs(None,root)
        
        queue = collections.deque([target.val])
        visited=set()
        visited.add(target.val)
        while K:
            for i in range(len(queue)):
                parent=queue.popleft()
                visited.add(parent)
                for child in graph[parent]:
                    if child not in visited:
                        queue.append(child)
            K-=1
        return list(queue)

BigO

We use DFS to construct the graph like dictionary will take O(n) and use BFS to iterate k level which will take less than O(n) in total the time complexity is roughly O(n)